Ejemplos de las Propiedades

Esperanza Matemática

Si una persona compra una papeleta en una rifa, en la que puede ganar 5000bs o un segundo premio de 2000bs con probabilidades de: 0.001 y 0.003. ¿ Cuál seria el precio justo a pagar por la papeleta?

• E(X)= 5000 . 0,001 + 2000 . 0,003 = 11bs 

Un jugador lanza dos monedas. Gana 1 o 2 bs si aparecen una o dos caras. Por otra parte pierde 5bs si no aparece cara. Determinar la esperanza matemática del juego y si este es favorable

• E(X)= {(C,C);(C,X);(X,C);(X,X)}

     p(+1)= 2/4
     p(+2)=1/4
     p(-5)=1/4

• E(X)= 1. 2/4 + 2 . 1/4 - 5 . 1/4= -1/4. Es desfavorable 

Varianza y Desviación Estándar 

1. Calcular la varianza de la distribución

9,38,8,9,8,9,18

2. Hallar la varianza y la desviación típica de la siguiente serie de datos:

12,6,7,3,15,10,18,5

 

3. Calcular la varianza de la siguiente gráfica

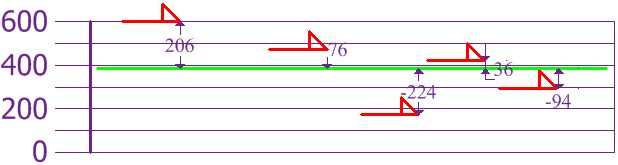
Varianza: σ2 =	2062 + 762 + (-224)2 + 362 + (-94)2	=	108,520	= 21,704
	5		5

Así que la varianza es 21,704

Y la desviación estándar es la raíz de la  varianza, así que:

Desviación estándar: σ = √21,704 = 147

Así que usando la desviación estándar tenemos una manera "estándar"  de saber que es "normal"